543. 二叉树的直径

2024-07-25 2024-07-26 约 200 字预计阅读 1 分钟

题目描述(力扣):

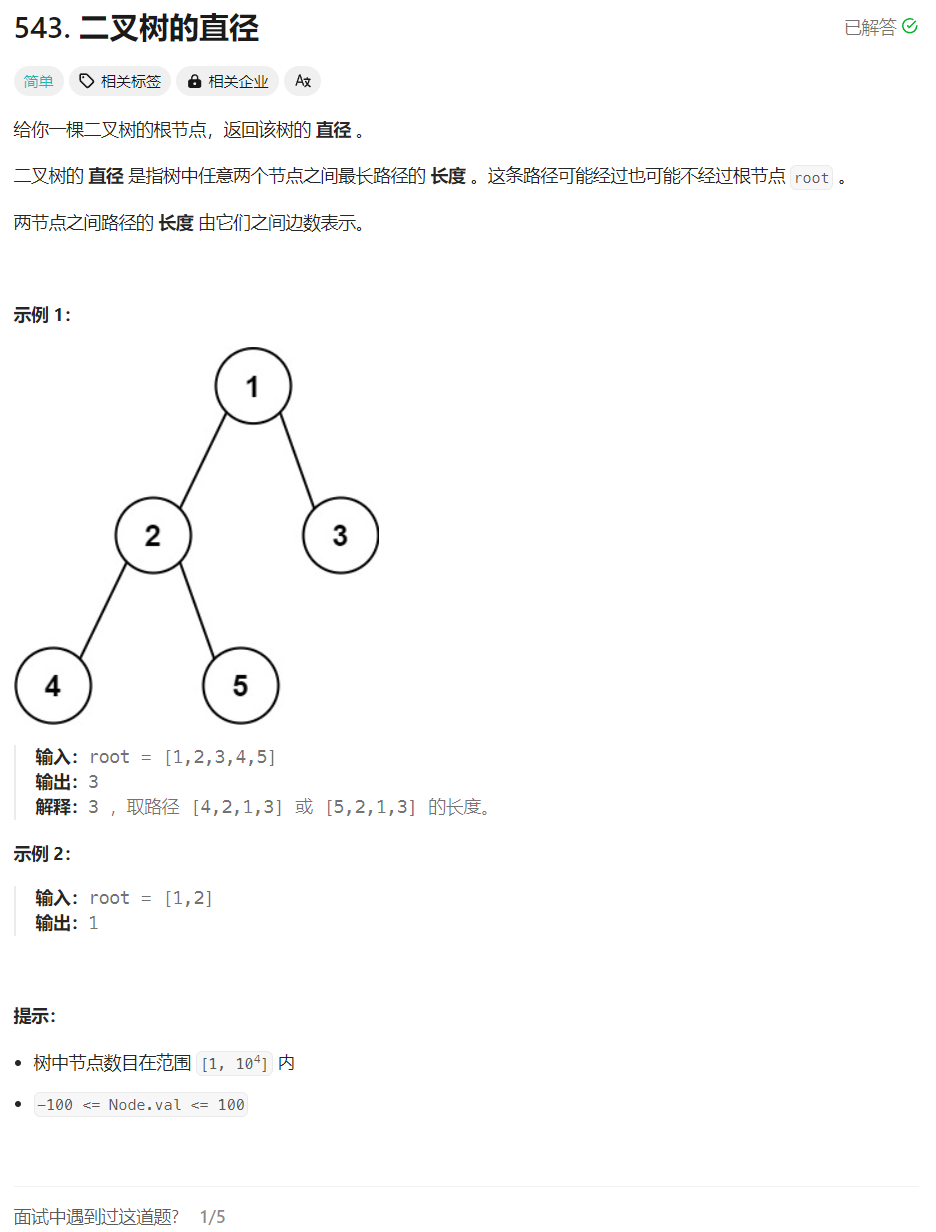
思路: 首先理解二叉树的直径指的是二叉树中任意两个节点之间的路径长度的最大值(最长直径不一定经过根节点)。想要找到二叉树的直径，就需要遍历每个节点，依次计算每个节点的左右子树深度之和，其中的最大值就是二叉树的直径。因为二叉树的直径大多数情况下就是根节点下的左右子树深度之和，但存在直径不经过根节点的情况，所以需要遍历每个节点，计算以该节点为根的二叉树的直径，然后取计算结果中的最大值。根据前面的分析，我们需要计算左右子树深度之和，这就需要左右子树的信息，所以选择后序遍历。

代码:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33


/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int diameterOfBinaryTree(TreeNode* root)
    {
        maxDepth(root);
        return maxDia;
    }

    int maxDepth(TreeNode* root)
    {
        if(root == nullptr) return 0;

        int lefth_h = maxDepth(root->left);
        int right_h = maxDepth(root->right);
        int Dia = lefth_h + right_h; //计算当前二叉树的直径
        maxDia = max(maxDia, Dia);

        return lefth_h > right_h? lefth_h + 1: right_h + 1; //返回子树高度
    }
private:
    int maxDia = -1; //用于存储二叉树直径
};