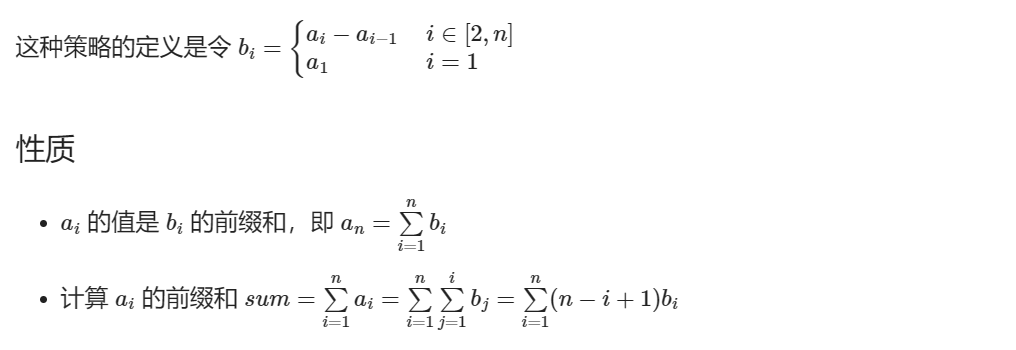思路
首先,搞一发暴力,对于每个查询的时刻,根据题目所给公式计算其核酸有效时间范围,判断计划出行时间是否在这个有效时间范围内。提交后发现果然超时,只能过7个样例。
暴力法是拿每个查询的时间去依次处理每个出行计划,再判断每个计划是否可以出行。想了一下,对于暴力法没有什么大的优化点,那么能不能逆向一下处理流程呢?先处理每个出行计划,计算出每个出行计划最早和最迟做核酸的时刻,再处理每个查询的时刻。当然可以!我们可以先将每个出行计划都转化成一个时刻区间 $[start, end]$ ,
- $start$表示要满足该出行计划的最早做核酸的时刻。
- $end$表示要满足该出行计划的最迟做核酸的时刻。
「只要开始做核酸的时刻$q$包含在该出行计划的时刻区间里,那么必定能满足该出行计划」。
通过上面的分析可知,可以用一个$time$数组存储每个时刻(下标$i$表示时刻i)被多少个出行计划所覆盖,那么在获取要查询的时刻$q$后,就可以直接返回$time[q]$,在$O(1)$的时间内就能知道该时刻做核酸能满足多少个出行计划。
但是修改时刻区间 $[start, end]$的每个时刻对应的值时(即修改每个$time[i],i \in [start, end]$),仍需遍历,最坏的时间复杂度仍然为$O(2 \times 10^5 \times m)$。有什么方法可以不用遍历就能让指定区间对应的值都加1呢?那就是差分法。这样一样,就可以在$O(1)$时间内让指定区间对应的每个值都加1。
那么来梳理一遍流程:
- 创建一个时刻数组 $time$,用来记录每个时刻被多少个出行计划所覆盖。
- 将每个出行计划转化成对应的时刻区间 $[start, end]$,使用差分法让time[i]都加1,其中$i \in [start, end]$。
- 查询时刻$q$时,直接返回$time[q]$。
差分法
差分法经常应用于「要将不同区间内的值都加上一个相同的值」。
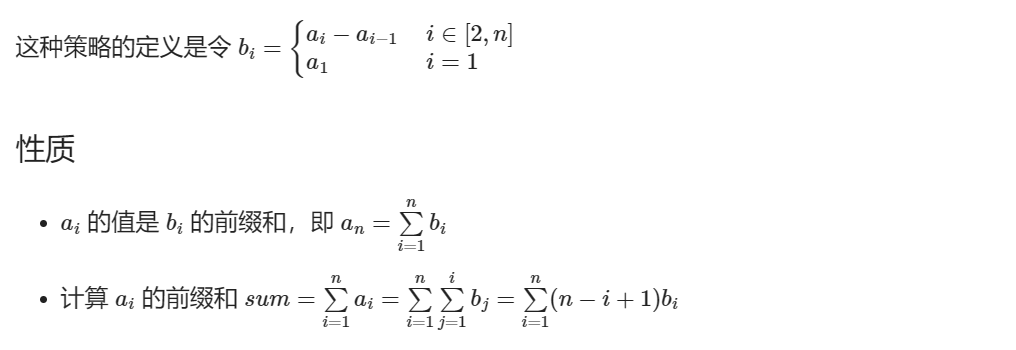
例如,将区间$[l, r]$的每个数都加上一个$k$,只需要让 $b[l] += k, b[r+1] -= k$; 这样就可以让$a_l$到$a_r$都加上$k$,因为$a_i$的值是$b_i$的前缀和。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
|
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int n, m, k, t, c, q, l, r;
int diff[200010] = { 0 }; // 构造差分数组, 因为time[i]的初始值均为0, 所以diff[i]也均为0
int main()
{
cin >> n >> m >> k;
for (int i = 0; i < n; ++i)
{
cin >> t >> c;
// 计算当前场所对应的时间区间
l = max(1, t - c - k + 1); // 计算进入该场所做核酸的最早时刻
r = t - k; // 计算进入该场所做核酸的最晚时刻
// 判断该场所是否能够进入
if (r > 0)
{
// 当前时间区间的每个时刻都加1, 即这个时间区间内的每个时刻能进的场所 +1
diff[l] += 1;
diff[r + 1] -= 1;
}
}
// 计算每个时刻能进的场所数
for (int i = 1; i <= 200000; ++i)
{
diff[i] += diff[i - 1]; // 这里直接用diff[i] 表示 time[i]了
}
while (m--)
{
cin >> q;
printf("%d\n", diff[q]);
}
return 0;
}
// 暴力法
// int n, m, k, flag = 0;
// int a[100010], b[100010];
// int main()
// {
// cin >> n >> m >> k;
// for (int i = 0; i < n; ++i)
// {
// cin >> a[i] >> b[i];
// if (a[i] <= k)
// {
// flag = i;
// }
// }
// int start, end;
// // 依次处理每个查询
// for (int i = 0; i < m; ++i)
// {
// int ans = 0;
// cin >> start;
// start += k; // 计算核酸有效的开始时间
// for (int i = flag; i < n; ++i)
// {
// end = start + b[i] - 1; // 计算核酸有效的最后时间
// if (a[i] >= start && a[i] <= end)
// {
// ++ans;
// }
// }
// printf("%d\n", ans);
// }
// return 0;
// }
|