题目 思路 直接暴力法，发现超时，怎么进一步优化呢？每个窗口我们都要从头到尾扫描一遍来寻找最大值，这是耗时所在，因为是寻找最大值，直接想到一种非常适合的数据结构——大根堆，堆顶就是最大值。每往右移动一次，就将新的元素加入堆中，再判断堆顶元素是否在窗口内，如果不是就移除，直到在当前窗口的元素成为堆顶。因为将一个元素加入到堆中的时间复杂度为$O(log n)$，所以算法的时间复杂度为$O(n log n)$。 能不能进一步优化呢？当然可以，在一个窗口中，假设两个元素的下标分别为$i, j$且$i < j$，那么「只要$i$在窗口中，$j$也必定在窗口中」。若$nums[i] < nums[j]$， 那么$nums[i]$必定不可能成为最大值，我们就可以不必存储类似$nums[i]$的值。所以，我们只需要用一个双端队列来存储「在当前窗口中可能在以后成为最大值的值的对应下标」。存储下标是因为我们后续要判断该值是否超过窗口范围。 根据前面的分析可知，该队列中的元素是递增的（因为是从左往后扫描的），元素(下标)对应的值是递减的。每次移动窗口就只需要将新元素与队尾元素对应的值进行比较，如果队尾元素对应的值小于新加元素对应的值，则将其移除（因为其对应的值不可能成为最大值了），不断地进行此项操作，直到队列为空或者新元素对应的值小于队尾元素对应值。 显然，队首元素对应的值就是当前窗口的最大值，但需要注意队首元素是否超过了窗口的范围。 这样我们只需要$O(n)$时间内就能完成此题。 代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 class Solution { public: vector<int> maxSlidingWindow(vector<int>& nums, int k) { deque<int> dq; // 初始化, 即处理第一个窗口中的值 for (int i = 0; i < k; ++i) { // 将不可能成为最大值的移除队列 while (!

题目 思路 直接暴力法，遍历每一个子数组查看其和是否为k，发现会超时。暴力法的时间复杂度为$O(n^2)$，瓶颈在于对于每个 $i$，我们需要枚举所有以$nums[i]$作为结尾的子数组来判断其和是否等于k，这一步是否可以优化呢？当然是可以的，考虑到子数组的连续性特性，可以通过 前缀和 来优化。 前缀和是指数组中从第一个元素到当前元素的和。假设 $pre[i]$ 为 $[0, …, i]$里所有数的和，那么 $pre[i]$ 就是前缀和。有了前缀和我们就可以用其来计算子数组的和, “子数组 [j, i] 的和为k” 就可以转化为以下等式： $$ pre[i] - pre[j - 1] = k $$ 通过变形就可以得到： $$ pre[i] - k = pre[j - 1] $$ 这说明，想要知道以 $nums[i]$ 结尾的和为 $k$ 的连续子数组的 个数 时只要统计在位置$i$之前有多少个前缀和为 $pre[i] - k$的$pre[j]$ 。所以，考虑建立哈希表，以前缀和为key，该前缀和出现次数为value，从左往右边更新哈希表边计算答案，即可在$O(n)$时间内完成此题。 需要注意的是，我们在构造哈希表时需要先插入键值对{0, 1} 且在遍历时必须先判断是否有符合条件的前缀和再往哈希表里记录当前前缀和。 为什么可以从左往右依次更新哈希表？ 因为$pre[i]$的值可以由 $pre[i - 1]$递推而来，即： $$ pre[i] = pre[i - 1] + nums[i] $$ 为什么在构造哈希表时需要先插入键值对{0, 1}? 这是为了处理特殊情况。当我们处理到位置 $i$ 时，我们想要知道的是全部以 $nums[i]$ 结尾的和为 $k$ 的连续子数组的个数，这肯定包括由[0, …, i]组成的连续子数组，它们的前缀和即为 $pre[i]$，如果不先插入键值对{0, 1}就会漏掉 $pre[i] = k$ 这一情况，导致漏算答案。

题目

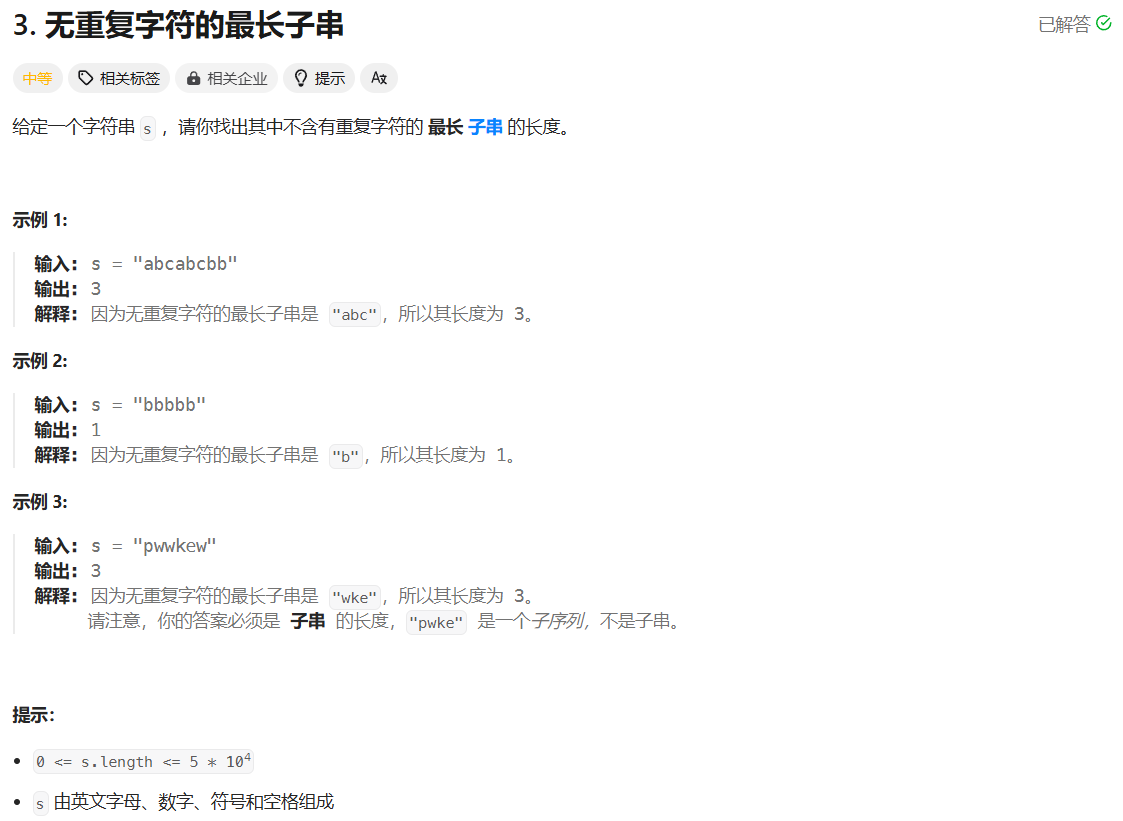
思路

使用两个指针$l, r$分别指向当前字串的左右边界，通过不断将 r 指针往后移使得子串不断变长，在移动r指针的同时需要判断新增的字符是否已经在窗口中出现了，如果已出现则需要移动l指针来将重复的字符移动出窗口，这样通过一次遍历就能找到无重复字符的最长子串。

代码

题目 思路 接的雨水总量为每个柱子能够接的雨水之和，而每个柱子的接水量计算公式为： $$ 接水量=\min(左右两边最高柱子)−当前柱子的高度 $$ 那么直接新建两个数组 left_max 和 right_max 来存储每个柱子左右两侧的最大高度， left_max[i] 和 right_max[i] 分别表示柱子i左右两侧的最高柱子高度( left_max[i] 从左往右计算， right_max[i] 从右往左计算)，然后再通过遍历计算每个柱子的接水量累加起来即可。 上面的方法时间复杂度和空间复杂度均为$O(n)$。时间已经是最快了，那么空间上还能不能进行优化呢？上面的方法空间耗费主要来自于新建的两个存储数组。由于数组left_max是从左往右计算，数组right_max是从右往左计算，因此可以使用双指针和两个变量代替两个数组。 对于左指针left来说，其左右两侧的最大高度分别为left_left_max和 left_right_max；同理右指针有right_left_max和 right_right_max。由于$right > left$，故$right\_left\_max \ge left\_left\_max$ 且 $left\_right\_max \ge right\_right\_max$，这两个不等式画个图便可直接看出。 由上面的不等式可知： 若$right\_right\_max > left\_left\_max$，则必有$left\_right\_max > left\_left\_max$，又left_left_max是可知的， 那么就可以计算left指向的柱子的接水量。 若$right\_right\_max < left\_left\_max$，则必有$right\_left\_max > right\_right\_max$，又right_right_max是可知的， 那么就可以计算right指向的柱子的接水量。 在处理了left指向的柱子后，++left向右移; 在处理了right指向的柱子后，--right向左移，直到全部柱子都被处理。 代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 class Solution { public: int trap(vector<int>& height) { int ans, left, left_max; int right, right_max; ans = left = 0; right = height.

题目 思路 题目中要求找到所有 「不重复」且和为0的三元组，这个「不重复」的要求使得无法直接使用三重循环枚举所有的三元组找到答案。当然，可以直接用三重循环枚举每个答案，再使用哈希表进行去重(即先对得到的答案进行排序，比如从小到大，再转化成string后存放进unordered_set)，得到最终答案。这种做法时间复杂度和空间复杂度都很高，因此需要换一种思路来考虑这个问题。 重复的答案形式为：$(a, b, c)、(a, c, b)、(b, a, c)$…… 假设$a \le b \le c$，如果能保证只有$(a, b, c)$这种形式的答案会被枚举，就能够直接去除掉重复的答案，而不必再使用哈希表来进行去重了。 要实现这一点，就可以通过将数组中的元素从小达到进行排序，随后使用三重循环进行遍历，且 「每重循环相邻两次枚举的元素不能相同」，否则也会造成重复。例如：一个排完序后的数组为$[-1, 0, 1, 1, 2, 3]$，第一次枚举到的三元组为$(-1, 0, 1)$ ，如果第三重循环继续枚举下一个相邻元素，那么仍然为 $(-1, 0, 1)$，这就产生了重复，因此就需要将第三重的循环跳到下一个不相同的元素，即数组中的最后一个元素3，枚举三元组$(-1, 0, 3)$。 至此，我们已经对初始版本进行了空间上的优化，下面给出伪代码： 1 2 3 4 5 6 7 8 9 10 nums.sort() for first = 0 .. n-1 // 只有和上一次枚举的元素不相同，我们才会进行枚举 if first == 0 or nums[first] != nums[first-1] then for second = first+1 .. n-1 if second == first+1 or nums[second] !

题目描述： 思路 时间复杂度为 $O(n^2)$ 的算法思路很简单，直接采用暴力法使用两层循环遍历每一种可能，判断是否存在答案。 这里详细说明一下时间复杂度为 $O(n)$ 的算法，暴力法之所以慢是因为寻找 target - x 的时间复杂度过高。那有没有什么方法可以加速寻找元素 target - x 是否存在且存在时可以知道其索引呢？有的，那就是使用哈希表来做，以target - x 为key，以索引为value。这样，寻找target - x的时间复杂度就变为了 $O(1)$，极大地提高了效率。 具体来说，对于遍历的每个元素，先判断其target - x是否存在，若存在，则直接返回对应的下标；若不存在，则将x存入哈希表，方便后续的查找。 代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 // 暴力法 class Solution { public: vector<int> twoSum(vector<int>& nums, int target) { for (int i = 0; i < nums.

前言 最近在看的一篇布局论文，发现其将 Mean Shift 算法扩展来进行聚类操作，而想要读懂文章就必须先理解此算法，故此文章记录的就是我对该算法的理解，若有理解错误的地方，欢迎留言指正。 简介 Mean Shift 是一种「基于密度」的聚类算法，它是一种非参数聚类方法（无需开始前指定簇数），可以自动从数据点的分布中推断出簇的数量。该算法会让数据点朝着密度更高的地方进行快速移动，直到达到该数据点所在区域的局部密度峰值地（即簇中心）。 通俗来说，将密度峰值比作山顶，数据点视为登山者，该算法就是让每个登山者沿着最快的路径登上离自己最近的山顶，登上同一个山顶的登山者就属于同一个簇。 带宽 带宽(bandwidth)是Mean Shift 算法唯一需要指定的参数，它用于确定每个点的邻域。以当前点为圆心，带宽为半径画圆，所画出的圆就是该点的邻域，在邻域内的点就是该点的邻居。 带宽非常重要，它会影响簇的大小： 小带宽。这会形成许多小簇，因为只有近距离的点才会形成一个群集。 大带宽。这会形成较少的大簇，因为距离远的点也可以形成一个群集。 核函数 在 Mean Shift 算法中，核函数的作用就是用来衡量当前移动点的邻居对该移动点的下一个位置的影响程度(由于该点是不断移动的，所以其邻居也会不断变化)。 为什么使用核函数？ 核函数有助于平滑数据并确保远离中心的点不会过度影响结果。它使得 Mean Shift 算法关注数据中的局部情况而不是全局，有助于进行分类。 核函数类型 核函数有非常多的类型，比如Uniform Kernel、Epanechnikov Kernel等，其中最常用的的是高斯核函数(Gaussian Kernel)： $$ K\left(\frac{x - x_i}{h}\right) = \exp\left(-\frac{||x - x_i||^2}{2h^2}\right) $$ $x$: 当前点坐标 $x_i$: 当前点的邻居坐标 $h$: 带宽 物理意义: 距离$x$越近的$x_i$，权重越大；超过带宽$h$的点权重为0 核密度估计(Kernel Density Estimation, KDE) 在Mean Shift算法中，KDE 的作用是用来估算数据点的局部密度分布。它通过核函数将每个点的邻域内的其他点进行加权，提供一个平滑的、连续的密度估计，帮助识别局部密度峰值(即告诉我们山顶在哪)，确定点的移动方向。KDE具体公式如下: $$ f(x) = \frac{1}{nh^d} \sum_{i=1}^{n} K\left(\frac{x - x_i}{h}\right) $$ $n$: 数据集中的点数 $h$: 带宽 $d$: 数据的维度 $K\left(\frac{x - x_i}{h}\right)$: 核函数，加权每个点 $x_i$ 对当前点的密度贡献 均值漂移向量(Mean Shift Vector) 在使用KDE确定了移动方向后，就需要使用均值漂移向量来将该数据点移动到当前的山顶。